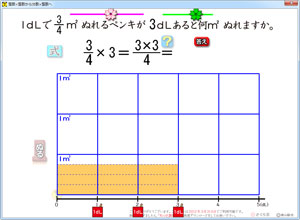
 ペンキの図です。
ペンキの図です。
教科書にも定番のように出てきます。
この図を使わなくても,分数×整数の理解(なぜ,分子×整数をするのか)は,できます。
その場合は,「ジュースが2/3Lあって,それが3つあったら,何L?」などといった,イメージしやすい問題を出します。
また,分母・分子を一言で説明できる状態に子ども達を伸ばしておきます。「分母は入れ物の目盛り」「分子は中身(ジュース)」という具合に。
このように,「目盛り」と「中身」と例えておくと,3つあるのは目盛りなのか中身なのか,簡単に分かります。もちろん,中身です。
だから,「中身(分子)×整数」となるのです。
しかし,それでもペンキ塗りのような図が教科書には登場してきます。6年生で学ぶ「分数×分数」に備えるためです。
×分数を理解するには,「単位分数でいくつ分」という頭の働きが必要です。そのために,「1がいくつ分」という姿(単位量あたりの大きさの考え方)がかけ算の姿なんだと示す必要があります。ペンキの図はそのためにとても便利な図なのです。(動けば,もっといいのですが・・)
このソフトがアップされたら,アニメーションをぜひご覧ください。動きます!!
動くので,子どもにとってちょっとわかりにくい教科書がとってもよく分かるようになるのです。
かけ算九九を学習した頃は,「かけられる数」という言い回しがありました。
分数のかけ算では,「元の数」「単位となっている数」「単位量」などと,言い回しを変える配慮があるとグッドです。「元」も「単」も,「1」という意味を持っているからです。
「かけられる」というのは行為から見た言い方です。分数のかけ算では,計算の仕組みを考えるので,この言い方は,ちょっと向きません。
