 6年の速さのソフトが仕上がったかのように見えたのですが,思わぬ失敗がみつかりました。
6年の速さのソフトが仕上がったかのように見えたのですが,思わぬ失敗がみつかりました。
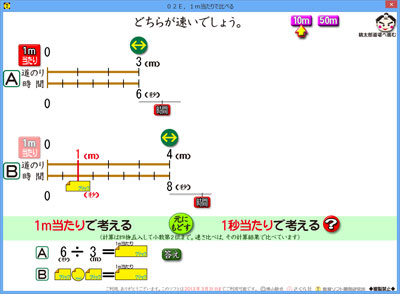
計算結果を小数第二位までの概数で求めているのですが,速さを比べるときには,どんどん割り進めた数値で比べていたのです。
そのため,答えは同じ数値になっているのに,判定ではBの方が速いなどと食い違いが出ていました。
こういうのは,算数・数学の持つ誤差によるズレです。これもなかなか大事な応用的理解につながります。
そこの修正手間取っていましたが,何とかプログラムを直せました。
--
ところで,上の画像のBの線分図。これをシンプルに書くと下のようになります。
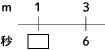
このシンプル線分図を作れるようになると,単位量あたりの問題はかなり簡単に解けるようになります。
線分図を見ながら考えれば,およそこのぐらいかなと概算できるからです。
きまりを見つけ出して,ちょっと変わった方法で解くこともできます。
線分図に,下のように田んぼの田の字のように枠を付けます。
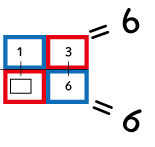
すると,斜めにかけた答えが同数になります。
赤×赤の答えと,青×青の答えが一致するのです。
なぜそうなるのかは,いうまでもありません。
この田んぼの田のような考え方は,3つの数から4つめの数を求める画期的な方法として,5,6世紀頃のインドですでに使われていました。ヨーロッパでも16世紀頃から普及した解法です。一般に「三数法」と呼ばれています。
三数法は,小学校で習う形式で言うと,比であり,大きさの等しい分数でもあります。
かけ算関係のたいていの問題は解けるのですが,解けないタイプもあるので,そこへの注意が必要です。
そうして,中学へ行くと方程式を習い,存在感がなくなる悲しい運命を持っています。
算数の歴史的なすぐれた思考法なのですが,将来性がないのが残念なところです。
