【横山験也のちょっと一休み】№.3769

子どもの頃、マッチ棒を使ったパズルで楽しんだことがありました。
この形をベースにして、問題が出題されていました。

問題①　マッチ棒を１本動かして、右向きの犬にしましょう。
問題②　マッチ棒を２本動かして、右向きの犬にしましょう。
問題③　マッチ棒を２本動かして、車にひかれた犬にしましょう。

子ども心に、何と面白い問題だと痛快な思いをしていました。

あれから、幾星霜。
５年生で「平行四辺形の面積の求め方」を学習します。その考え方が、この犬のマッチ棒パズルに似ていると感じていました。
そこで、ある時、この単元に入る直前に類似の問題を出題してみました。

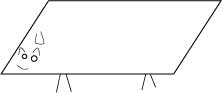問題　平行四辺形の紙を１回だけまっすぐに切って、動かして、犬の体の向きを逆向きにしましょう。

子ども達は面白がり、ほどなく正解を見つける子が出てきます。

顔の部分だけを切り取って右に移動すれば、犬が振り返っている姿になっているので、犬の体は逆向きになります。

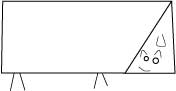そうして、この犬の名前を「平行四辺形ワンチャン」と言うことを伝えます。

これで準備は万端。
後は、平行四辺形の面積の単元に入ったら、教科書通りに流しても、授業の途中で、ワンチャンを思い出す子が出てきて、授業は愉快な雰囲気になり、新しい形の平行四辺形と、既習の長方形のつながりが強烈に印象づきます。

蛇足ですが、このような切って移動するやり方を等積移動と言います。等積移動の考え方は、面積は切ってつないでも保存されると言うことが、暗黙の了解で成り立っている考え方です。
ここから、曲げても丸めても面積は保存されると拡張していくと、さらに面白い授業を演出できます。面積を考えるところは、奥が深いです。

—
「平行四辺形ワンチャン」は緑の本に載っています。
まだ、お持ちでない先生、この機会にぜひ！