【横山験也のちょっと一休み】№.3772
算数の話を一つ。
三角形の内角の和を考える場面の話です。
考え方として、3つの方法があります。
1,みんなでいろいろな三角形の角を実際に測って、180度だとする方法
2,三角形の紙を切って、並べ替えると、3つの角が直線になるという方法
3,三角形の紙をうまいこと折って、3つの角が直線になるという方法
この中の3つ目は、次第に姿を消しているのですが、私は面白い方法と、感心ていました。
どんな方法か、よくわからない先生もいると思いますので、簡単な図を載せることにします。
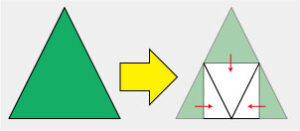
このやり方は、私も授業で子供たちに紹介しました。
紹介するときには、色の違う紙で同じサイズの三角形を作っておきます。
2枚の三角形を、その中央部分だけにのり付けします。
すると、下の紙が折る前の様子を表し、上の紙は折った後の姿となります。
こうすることで、折った後の角が、折る前のどの角と対応しているかがすぐにわかります。
折る前の姿と折った後の姿。
この前後の姿を同時に見せることが、理解を助ける一つの方法となります。
同様の方法は、展開図の学習でも行っていました。
この考え方のルーツは、分数の紙です。分数は「3つに分けた1つ分」というように、分けたという過去と、1つ分という現在を、同時に示しています。
次元の異なるものを1つにして表現しているからか、分数は、小数には無い面白さを持っています。
ところで、先ほどの図をよく見ると、面白いことに気が付きます。
面積という視点で見てください。
三角形の面積の求め方として、新たな世界が見えてきませんか。
少々面倒なやり方ですが、論理的に成り立ちます。これを言ってくる子がいたら、すごい子だろうなと思います。
—
下の3冊は、私が書いた算数のアイディア教材集です。どれも面白いです!
 |
 |
 |
