三省堂本店で,有田和正先生とお話しをさせていただいた時,算数の大雑把な話をしました。
----
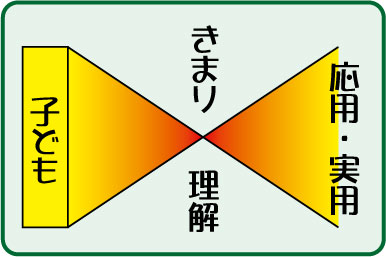
算数は「きまり」に向かって進みます。
その後,応用や実用といった広がりを持ちます。
----
基本的に,この「きまり」→「応用・実用」が繰り返されます。
角度や面積など,軽く思い出すだけでも,この流れになっていることがわかります。
大筋,こんな風なことなのだと分かっていると,頭は少しスッキリします。
「きまり」に向かうときには,広がりを求める活動はしてはいけないのだと,簡単に分かるからです。操作学習や体験学習をすると,子ども達はあれこれと気づきが生じます。
面白い発見もでてきます。
でも,目をつぶります。めざすは,「きまり」だからです。
昔の戦に例えれば,「きまり」という大将の首をとることを目指せばいいのです。
雑魚を何人やっつけても,価値がないのが算数です。
算数ソフトは「きまり」を見つける学習に非常に力を発揮します。
ソフトを見ている内に,「あっ!分かった」とか「ああ,そういうことか」と自分なりにきまりを理解していきます。
自分で見いだすと,不思議と伝えたくなります。
「こういうことでしょ!」とか,「だって,こうなってるじゃん」と。
自分で見つけたきまりは,実に素朴です。
それを表現させると,くどくなったり,あらっぽくなったりします。
でも,この「素朴なきまり」は,とても大切です。
根源的な原理を正しく把握しているからです。
ただ,その表現がお粗末なのです。
言語化で後れを取っているのです。
ここまでつかめると,言語化を高める手立てを,考えればよいことに気がついてきます。
自分なりの「素朴なきまり」きまりを,ノートに記述させます。
稚拙でOKです。
それから,教科書の定義と見比べさせます。
教科書の言葉のシャープさが際だって見えてきます。
必要最小限の言葉で,誤解の無いように書く。
究極の達意の文章。
それを学べます。
有田先生とのお話の中で,きまりの理解の部分を「きまり」から「感覚」「体得」へと話しました。
ここも算数の大切な所です。後日,記します。