【横山験也のちょっと一休み】№.3773

ジョナサンの会で佐々木先生が紹介してくれた面積の問題。色のついた部分の面積を求めるのですが、これにかかわる話を少しします。

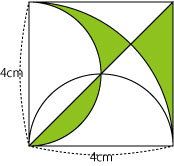この問題、その図形の面白さもあり、皆さん取り組み始めました。

すぐに、解答してきたのは中学理科の小川校長。あっという間の正解でした。
それからしばらくして、私が正解を出し、そのあと、また一人が正解を出し・・・
となりました。

この日は、私から、「教師の知る範囲で、子どもは思考する」という仮説の話をしていました。
この話と、この面積問題の取り組みがからみ、「一人が突破すると、後続がでる」（小川仮説）ということも話題になりました。

昔のサークルでしたら、こういう問題が出たら、これをどう子どもたちに教えるか、特にわかりやすい解き方が話題になっていました。これも、面白いのですが、今回は、集団文化論として、取り組みをとらえるかがちょっとした話題となりました。

問題が出てきたとき、それを解こうと取り組むか、無視するかは自由です。
どっちの立ち位置でも、個人としては本人の望む選択となります。
しかしながら、その場がジョナサンという集団であるため、二人ぐらいが取り組み始めると、自然と流れが生じます。この二人の中に集団のリーダー的な人がいると、解かないでいようと思った人でも、この流れが気になり、やっぱり解くかとなります。
気が付くと、全体が解こうとする方向に流れていきます。

学級でも同様の傾向になります。何人かが取り組み始めると、その中にクラスのリーダー的な子がいると、取り組む方向に流れが生じ、みんなやるようになります。
集団文化を意識する先生は、ここで注目すべきポイントがわかるので、かなり自動的に取り組む方向に流れていきます。

ここまでは、集団文化の流れですので、皆さん、大筋の把握はできています。
今回は、これに「一人が突破すると、後続がでる」という小川仮説がかぶさってきました。
これは面白い課題です。何かの折に、書いていきたいと思います。

ところで、先の問題。計算してはいけません。まずは動かすのです。
—

下の３冊は、私が書いた算数のアイディア教材集です。どれも面白いです！