【横山験也のちょっと一休み】№.3774

先日紹介した、佐々木先生のレポートにあった面積の問題。
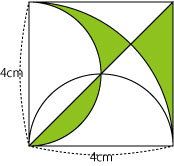この問題を紹介して、「計算してはいけません。まずは動かすのです」と書きました。
でも、解き方を書いておくのも大切かと思い、改めて書いていきます。

下のように、動かします。


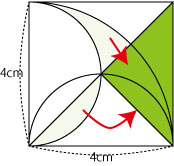
すると、三角形が浮かび上がります。
この三角形は、全体の1/4の広さを持っているので、面積は（４×４）÷４＝４です。

このように書くと、いかにも私はスラスラ解けましたと言っているように思えてきます。が、実際はスラスラとはちょっと遠い感じでした。
佐々木先生のレポートを見て、解き始めたのですが・・・。

まずは、ここはこんな風に計算して、こちらはこんな感じかな・・・という計算の仕方で思考をしていました。
しかし、それでは困難が大きかったので、途中でやめて、方向転換しました。
図形を動かすことをやってみたら、偶発的にいい形になりました。

これが現状なのですが、こういうところに、ふと思いを寄せると、ちょっとした人生の面白さを感じます。

最初に思い付いた方法で頑張り貫いて成功すると、「一貫した取り組みが功を奏する！」とか、「初心貫徹！」などと、変化せずに頑張りぬくことの大切さが強く感じ取れてきます。「貫く」という言葉にただそれだけで貴重な姿勢と、その維持の大切さを感じます。「吾道一以貫之」（論語）も思い出されます。

ところが、今回の私のように、転じて進んでうまくいった場合は、「あの手この手が大事！」とか、場合によっては、「やはり、虱潰しこそ命！」などと思いやすくなります。「唯一生き残るのは変化できるものである」とダーウィンも言っています。

成功までの過程がどういう状態かは、時々の状況によって決まってきます。一貫が大事と日ごろから口にしている人でも、方向転換をすることも多々あります。
逆に、いろいろやることが大事と思ってる人でも、一つ目の思考でうまくいってしまうこともあります。

自分の生活でも、貫くことでうまくいくこともあれば、転じることでうまくいくこともあります。どっちも、時の運のようなものなのです。
そんなところから、このような難問を出題して取り組んだ時には、考え方が途中で変わったかどうかを聞いてみるのも、楽しいです。教師として、一味違う言葉かけができますね。

—
こちらの本には算数の面白い教材アイディアがたくさん載っています。
まずは、１冊、読んでいただけると嬉しいです。