鶴亀算の話

【横山験也のちょっと一休み】№.3788

昔懐かしい「鶴亀算」の話をしましょう。

鶴と亀が合わせて５匹います。
足の数は全部で１４。
さて、鶴と亀はそれぞれ何匹いるでしょう。

このような問題です。
単純に、５＋１４とか、５×１４とすれば解けるような問題ではありません。
ですので、小学生のころ、どうにもよくわからず、苦戦していました。

すると、わかっている人が、「全部鶴と考えて・・」と解説をはじめます。

この解説が私にはいただけませんでした。
「もし、全部鶴だったら」という仮定の話なので、私の頭は「全部は鶴じゃない。亀もいる」となってしまいます。問題の設定から離れることを認めることができませんでした。

算数は具体から離れて考える学問なのですが、そうは言っても、鶴と亀はいるのだからと、そこから離れることは、してはいけないことのように思えたのでしょう。

そんな私だったのですが、面白い解き方を教えてくれた人がいました。

「全部で５匹なんだから・・・」と言いつつ、丸を５つかきます。
続けて、「この丸に足を２本ずつつけると、こうなる。」
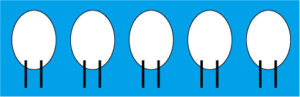そうして、「足は全部で１４本だから、あと４本あるから、足を付け足して、こうなる。」
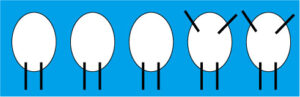「だから、亀は２匹、鶴は３匹。おしまい」

この解説は、妙に納得しました。
仮定が無いからです。仮定をしているのでしょうが、それを言わないのです。
この仮定の隠蔽が、頭への伝わりをよくしてくれるのです。

面白いのは、理屈抜きで頭に伝わったこの手順が、問題とちょっと離れているので、それを自分で関係づけようとすることです。
要するに、後から理由を考えているのです。

こんなことを書いていたら、ふと、清水一家の話を思い出しました。
清水の次郎長の子分・森の石松の話です。
船中で自分のことをほめた客がいたので、その客に石松が言います。
「江戸っ子だってねぇ。酒飲みねー、寿司くいねー」
こういううれしい時の、理屈のつながらない論法、喜び論法。私は妙に好きです。
うれしさ増して、理屈が消え、江戸っ子は酒＋寿司なのです。

小学生に教えるとき、理屈を通した方が分かりやすい子もいますが、私のような鈍もいます。
そういう時は、こういう詳しい解説抜きで、「こうやったら、こうなるじゃん」で進んだ方が、案外、その後、自分で考えたりするものです。

—
下は、算数の授業のアイディアを満載した、ちょっと面白い本です。
是非、お読みいただけたらと願っています。