【横山験也のちょっと一休み】№.3783
数学の一般書を読んでいたら、わり算のあまりの考え方がIDやパスワードなどの暗号に使われていると出てきて驚いたことがあります。
その解説を読むと、素数の話になり、次第に頭が遠のくのですが、それでも、３年生で教える、あのわり算の「あまり」が「暗号」として使われているなんて、何とも言えない喜びを感じます。
算数で暗号といえば、位置の表し方で登場してきます。
座標があって、その座標中に文字が書いてあり、それを指示文（２，４）→（５，１）などと辿って行って、どんな文ができるか楽しみます。
同様のことを、約分でも楽しむことができます。
例えば、次のような問題です。
あまね
－－－＝
ねあ
同じ平仮名を約して１にすると、分子の「ま」が残るので、答えは「ま」となります。
平仮名での出題は、同じ文字を１にしていくタイプなので、算数で表すと、次のようなタイプの問題となります。
３×７×２
－－－－－＝
２×３
これもいいのですが、約分らしさがありません。
数を分解して約するところが、約分の一番の醍醐味ですので、
４×９
－－－
６×２
と、このようなタイプの方がより約分の学習にフィットした暗号になります。
そこで、平仮名でなく、漢字にすると約分らしさが高まります。
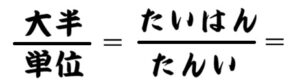平仮名が漢字の因数のようになるので、約分らしい雰囲気が高まります。
答えとしては、「は」が残ります。
ところで、約分ですが、この「約」を調べたことがありますか。
訓読みにすると、「約（つづ）める」とか「約（つづ）まる」となります。要するに、簡潔にすることです。
ですので、「約分」をその漢字から考えると「分けて、簡単にすること！」となります。
何を分けるかというと、数を分けます。
小学校で習う数の分け方には、２種類あり、一つはたし算タイプ。もう一つはかけ算タイプです。
こんなことを、子どもたちにちょっと話して、「約分」の意味を漢字から考えてもらうのも楽しい学びになりますね。
—
こちらの３冊には、楽しい算数の教材アイディアがたくさん載っています。
 |
 |
 |